前回の回答

前回の宿題の回答から

ボールを水に投げ込んだときのような様子をアニメーションにしてみましょう。

問題はこうでしたね。

これは、そんなに難しくなく解けたのではないでしょうか。

const main = () =＞ {
  const canvas = document.getElementById(’canvas’);
  const ctx = canvas.getContext(’2d’);


  // -------------- 計算用定数定義 -------------- //
  // 開始時点の時間を取得しておく
  const init_time = new Date();

  // ボールの半径
  const r = 10;

  // ボールの初期座標(画面外上側からスタート)
  const x = 200;
  const y = -10;

  // ボールの初速度
  const v0x = 0;
  const v0y = 80;

  // 加速度(マイナスにする)
  const a = -10;

   // -------------- 描画処理 -------------- //
  const draw = () =＞ {
    ctx.fillStyle = ’rgb(179, 229, 252)’;
    ctx.fillRect(0, 0, 640, 480);
    // 現在時刻を取得
    const now = new Date();
    // 開始時点から現在までの経過時間
    const diffSecond = (now.getTime() - init_time.getTime()) * 0.01;

    // 現在の x 軸方向の位置
    const px = x + (v0x * diffSecond);

    // 現在の y 軸方向の位置
    const py = y + ((v0y * diffSecond) + (0.5 * a * diffSecond * diffSecond));

    ctx.fillStyle = ’rgb(63, 81, 181)’;
    ctx.beginPath();
    ctx.arc(px, py, r, 0, Math.PI*2, false)
    ctx.fill();

    // 次回画面更新時に draw を実行するように指定
    requestAnimationFrame(draw);
  };

  // 一回目描画実行
  draw();
};

document.addEventListener(’DOMContentLoaded’, main);

最初の定数を、

スタート地点が画面の上側からとなるように、 y にマイナスの値を付与
最初は下向きに動くように、y 方向の初速度はブラスの値にする
重力と逆方向に加速度がかかるので、加速度もマイナスに変更

これで、それっぽいアニメーションができますね。

背景は clearRect を fillRect に変えて、
画面全体を水色で塗りつぶしてしまえば OK ですよね！

いかがでしたでしょうか。

ボールのバウンドを表現！…の前に、計算の仕方を少し変更

さて、前回は投げられたボールをアニメーションで表現してみました。

今回は、そこに少しだけ手を加えて、ボールが画面内でバウンドするようにしてみましょう。

…なのですが、今回以降の内容を実施するに当たって、
すこしばかり計算の仕方を変更しようと思います。

というのも、前回の計算は
「ボールが投げられた後、何も周りから影響を受けない場合」の計算の仕方だったんですね。

今回のように、投げられた後に何かしらの影響を外部から受ける場合には、
前回の計算方法はちょっと適しません。

なにが問題かといいますと、

    // 現在の x 軸方向の位置
    const px = x + (v0x * diffSecond);

こういった計算。
この、 v0x の所です。

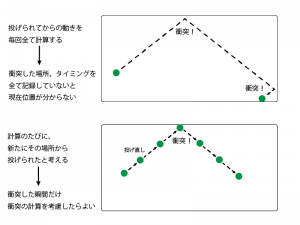
この計算では毎回投げられたところからのボールの挙動を全て計算しているのですね。

こうすると、例えば今回のように壁にぶつかることを考えるとき、
いつ、どこで壁にぶつかったかを全て記録し、毎回計算上で考慮しなければなりません。

それは面倒ですよね？

ということで、ちょっと計算の考え方を変えます。

これまでは、投げられたところから何秒後にどこにボールがあるかを計算して描画していましたが、
今回からは、画面を書き直すごとに、「ボールを投げ直す」と考えましょう。

こうすることによって、壁に衝突した瞬間のみ、衝突について考えれば良いようになります。
そのほかのタイミングでは、前回描画した地点からの進みだけを考えれば良いので、
とてもラクで、シンプルになりますね。

実際にシミュレーションを作る場合は、
前回の方法では時間が経過して行くにつれて計算量が膨大になってしまうため、
このように前回からの差分を計算するような方法をとることがよくあります。

ということで、前回の内容を投げ直しで考えたときのコードがこちら。

const main = () =＞ {
  const canvas = document.getElementById(’canvas’);
  const ctx = canvas.getContext(’2d’);


  // -------------- 計算用定数定義 -------------- //
  // 開始時点の時間を取得しておく
  let prev_time = new Date();

  // ボールの半径
  const r = 10;

  // ボールの初期座標
  let x = 50;
  let y = 440;

  // ボールの初速度
  let vx = 30;
  let vy = -80;

  // 重力加速度
  const a = 10;

   // -------------- 描画処理 -------------- //
  const draw = () =＞ {
    ctx.clearRect(0, 0, 640, 480);
    // 現在時刻を取得
    const now = new Date();
    // 開始時点から現在までの経過時間
    const diffSecond = (now.getTime() - prev_time.getTime()) * 0.01;

    // 次の計算に備えて、 prev_time に now を代入
    prev_time = now;

    // 現在の x 軸方向の位置
    x = x + (vx * diffSecond);

    // 現在の y 軸方向の位置
    y = y + ((vy * diffSecond) + (0.5 * a * diffSecond * diffSecond));
    vy = vy + (a * diffSecond);

    ctx.fillStyle = ’rgb(63, 81, 181)’;
    ctx.beginPath();
    ctx.arc(x, y, r, 0, Math.PI*2, false)
    ctx.fill();

    // 次回画面更新時に draw を実行するように指定
    requestAnimationFrame(draw);
  };

  // 一回目描画実行
  draw();
};

document.addEventListener(’DOMContentLoaded’, main);

コードを実行してもらったら、前回と同様の動きをすることが分かるかと思います。

ポイントはここ

    // 次の計算に備えて、 prev_time に now を代入
    prev_time = now;

前回は、毎回の計算でアニメーション開始時点の時間からの経過時間を取得して計算していましたが、
今回は、計算後に、開始時間を更新していくことで、スタートの時間が更新されていきます。

もう一点はここ。

vy = vy + (a * diffSecond);

計算のたびに、現在の速度を計算しなおして、初速度を更新していますね。

ちなみに、ここで出てきた式は

現在の速度 v は初速度 v0 に a × t (a は加速度・t は時間)を足したものという式になります。
前回、一定の時間でどれだけ速度が変化するかというものを表したものが加速度とお話をしましたので、
逆に、加速度に時間をかければ、その時間で速度がどれだけ変化したかという値になりますね。

以上で、計算の方法を変更することができました！

ボールがバウンドする処理を追加する

さて、本題のバウンドに入っていきましょう。

とは言っても、考えることはとても簡単です。
ボールのバウンドでは、「作用・反作用の法則」をそのまま適用することができます。

作用・反作用の法則とは、物体 A が他の物体 B に力を加えるとき、A が B に与える力と同じ大きさの力を、B が A に与えるという内容ですね。

…と、定義通りの言葉を書いてもいまいち分からないので、今回の場合で考えてみましょう。

今回は、ボールのバウンド、すなわちボールがが壁にぶつかる時を考えます。

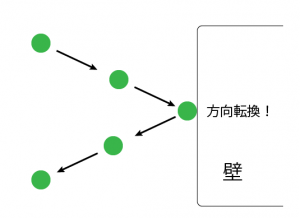
飛んできたボールが壁にぶつかる前後から図に表してみました。
この図を見ると、（当然ですが）ボールは壁にぶつかった瞬間に方向転換していますね。
また、その以外の、壁にぶつかっていない時は、これまで通り急な方向転換などはなく飛んでいきますね。

以上のことから、ボールは

壁にぶつかった瞬間に、ボールは何かしらの力を受ける
壁にぶつかっていない時はボールには力がかかっていない

ということが分かります。
つまり、ボールのバウンドを考えたい場合、ボールが壁にぶつかった瞬間だけ注意していればよいということですね。

では、この壁にぶつかった時にボールはどんな力を受けているのでしょうか。

実はこれは簡単です。
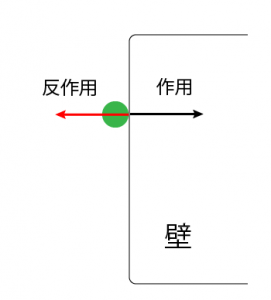
ボールが壁にぶつかった瞬間、ボールは壁を押します。（これが作用です）
これと同じ大きさの力で、壁はボールを押し返すのです。（これが反作用ですね）
これが作用・反作用の法則ですね。
後は詳しいことは調べてもらったら色々丁寧な解説がでますのでそちらで…

さて、作用・反作用の法則から、ボールが壁にぶつかった時、壁を押す力と同じ力でボールは押され返すということが分かりました。
同じ力で押し返されるということは、動きも反転するということになるますね。

ということで、ボールが壁にぶつかった瞬間、ぶつかった方向の速度を反転してあげたら良いですね。

以上を踏まえてコードを書きましょう。

const main = () =＞ {
  const canvas = document.getElementById(’canvas’);
  const ctx = canvas.getContext(’2d’);


  // -------------- 計算用定数定義 -------------- //
  // 開始時点の時間を取得しておく
  let prev_time = new Date();

  // ボールの半径
  const r = 10;

  // ボールの初期座標
  let x = 50;
  let y = 440;

  // ボールの初速度
  let vx = 30;
  let vy = -80;

  // 重力加速度
  const a = 10;

   // -------------- 描画処理 -------------- //
  const draw = () =＞ {
    ctx.clearRect(0, 0, 640, 480);
    // 現在時刻を取得
    const now = new Date();
    // 開始時点から現在までの経過時間
    const diffSecond = (now.getTime() - prev_time.getTime()) * 0.01;

    // 次の計算に備えて、 prev_time に now を代入
    prev_time = now;

    // 現在の x 軸方向の位置
    x = x + (vx * diffSecond);

    // 横方向に飛び出していたら、壁にぶつかっていると判定
    if (x &lt; 0) {
      x = -x;  // 壁から飛び出した分を戻す
      vx = -vx;  // 動きを反転
    }
    else if (x ＞ 640) {
      x = 640 - (x - 640);  // 壁から飛び出した分を戻す
      vx = -vx;  // 動きを反転
    }

    // 現在の y 軸方向の位置
    y = y + ((vy * diffSecond) + (0.5 * a * diffSecond * diffSecond));

    // 下方向に飛び出していたら、床にぶつかっていると判定
    if (y ＞ 480) {
      y = 480 - (y - 480); // 床から飛び出した分を戻す
      vy = -vy;  // 動きを反転
    }
    else {
      vy = vy + (a * diffSecond);  // 床にぶつかっていない時は通常通りの動きをさせる
    }

    ctx.fillStyle = ’rgb(63, 81, 181)’;
    ctx.beginPath();
    ctx.arc(x, y, r, 0, Math.PI*2, false)
    ctx.fill();

    // 次回画面更新時に draw を実行するように指定
    requestAnimationFrame(draw);
  };

  // 一回目描画実行
  draw();
};

document.addEventListener(’DOMContentLoaded’, main);

ボールが枠内でバウンドして戻ってくるようになりましたね！

追加されたのはここ。

    // 横方向に飛び出していたら、壁にぶつかっていると判定
    if (x &lt; 0) {
      x = -x;  // 壁から飛び出した分を戻す
      vx = -vx;  // 動きを反転
    }
    else if (x ＞ 640) {
      x = 640 - (x - 640);  // 壁から飛び出した分を戻す
      vx = -vx;  // 動きを反転
    }

壁にぶつかった瞬間だけ考えればよいので、
計算する瞬間に、このまま進んでいると壁を突き抜けていないかを確認します。

突き抜けている場合、まずはその分だけ壁の手前側に戻してあげましょう。
その後、速度を反転させます。
先ほど考えたように壁にぶつかったボールは作用・反作用の法則に従って
ぶつかるときと同じ速度で逆方向に動きますので、これだけでいいですね。

速度を反転させることで、以後の計算では逆向きにボールがうごいていくことになります。

床方向も同じですね

    // 下方向に飛び出していたら、床にぶつかっていると判定
    if (y ＞ 480) {
      y = 480 - (y - 480); // 床から飛び出した分を戻す
      vy = -vy;  // 動きを反転
    }
    else {
      vy = vy + (a * diffSecond);  // 床にぶつかっていない時は通常通りの動きをさせる
    }

常に重力はかかっているのですが、今回は反転する瞬間は純粋に作用・反作用の法則に従った動きにしたかったため、
動きを反転させる場合とそうでない場合で速度の処理を分けています。

意外にとっても簡単に実装できましたね！