前回の回答

前回の回答から行きましょう。

前回の宿題は

• 以下のように、近づいて右下に抜けていくように見える円のアニメーションを作成してください

これでしたね。

イメージとしてはこんな挙動。

回答はこちら。

const main = () =＞ {
  const canvas = document.getElementById(’canvas’);
  const ctx = canvas.getContext(’2d’);
  ctx.fillStyle = ’rgb(63, 81, 181)’;

  // 開始時点の時間を取得しておく
  let prev_time = new Date();

  // 開始時点の x 座標を設定しておく
  let x = 50;
  let y = 50;
  let r = 10;

  const draw = () =＞ {
    ctx.clearRect(0, 0, 640, 480);

    // 現在時刻を取得
    const now = new Date();

    // 開始時点から現在まで、何ミリ秒経過しているかを計算
    const diffMillisecond = now.getTime() - prev_time.getTime();
    // 前回地点 + (経過ミリ秒 * 0.2) で、現在位置を算出
    x = x + (diffMillisecond * 0.2);
    y = y + (diffMillisecond * 0.2);
    r = r + 1;

    ctx.beginPath();
    ctx.arc(x, y, r, 0, Math.PI*2, false)
    ctx.fill();

    // 次回の実行のために、今回の時間を記録しておく
    prev_time = now;

    // 次回画面更新時に draw を実行するように指定
    requestAnimationFrame(draw);
  };

  // 一回目描画実行
  draw();
};

document.addEventListener(’DOMContentLoaded’, main);

前回のサンプルから、 y 方向の値と r (半径) の値を増加していくように設定したら良いだけでしたね。
簡単でしたか？

物理アニメーションやってみよう！

さて、お待たせいたしました。
今回のテーマである、物理アニメーションを作っていきましょう！

まずはとても簡単なところで、投げられたボールの動きを再現しましょう。

完成形からお見せすると、こちら。

たったこれだけ？と思いましたか！
まずはとても簡単な例から考えてみましょう。

式を考える

物理アニメーションで最も重要なのは、
物理現象を再現する式を正しく作ることです。

とは言っても、とても難しい事をするわけではありません。
特に、ゲームなどでは動きを完全に、正確に表現する必要はありません。
大まかに正しい動きができれば良いので、割と単純な式だけでもそれっぽい挙動を表すことができます。

さて、ここからガッツリと物理の話に入っていきますよ。

今回考える物理現象は、投げられたボールの動きですね。
ボールの速度について考えます。

まず知っておいてほしいのは、平面上でものの動きを考えるとき、
どんな方向の動きであっても二つの直交する動きの合成で考えられるということです。

小難しい表現ですね。図で考えましょう。
下の図で、ボールが点 A から点 B へ移動しています。ボールははナナメに動いてますね。
この動きについて、直接ナナメ方向に ○○ メートル動いた…と考えても良いのですが、
横方向に ○○ メートル動いて、縦方向に ○○ メートル動いたから、
それをあわせて、結果ナナメ方向に ○○ メートル動いた、と考えてもよい、ということです。

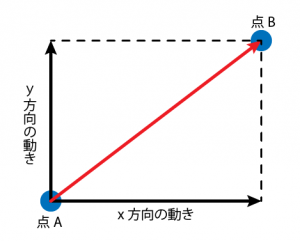
canvas で図形を描画する際には、これまで学んできたように x 方向・y 方向それぞれの位置を
指定することで任意の位置に図形を描画しましたよね。

また、後の利便性の兼ね合いもあって、今回は横(x 方向) と縦(y 方向)に分解して
動きを考えていきましょう。

無重力状態だとどうなる？

さて、早速ボールの挙動を…と行きたいところですが、その前に。
先ほどのアニメーションでは当然のように地球上での
ボールの動きをシミュレーションしようとしていました。
これが宇宙空間、すなわち無重力の環境でボールを投げるとどうなるでしょうか。

なんとなくイメージつきますよね？
多分こんな感じじゃないでしょうか。

先ほどの、地球上でのボールの動きのアニメーションとどう違うでしょうか？
簡単ですね。ボールが落ちてこないのです。

そして、とても大切なポイントが実はこの無重力環境でのボール投げアニメーションには含まれています。

そのポイントとは、（少し分かりづらいのですが）ボールの速度が常に一定であり、
進行方向も一定であるということ。
では、なぜボールの動きは一定になるのでしょうか？

これも実は簡単なことで、投げられた後のボールには一切の力がかかっていないからですね。

我々が見ることができる現象としてはカーリングがイメージしやすいですね。
カーリングのストーンは投げられた後、ほぼ一定の速度でまっすぐ進みます。
もちろん、氷とストーンの間の摩擦や空気抵抗などがあるので実際にはどこかで止まるのですが、
そういった摩擦などの影響が少ない環境では、物体が一定の速度で動こうとしているのを、なんとなく理解できるかと思います。

では地球上でのボールの挙動は？

さて、先ほどの宇宙空間でのボールのシミュレーションから、
外から力がかかっていない物体は一定の速度を保とうとする事が分かりました。

では、地球上でのボールの挙動はどうでしょうか？

これは先ほど上でもお見せしたアニメーションですが、
下に落ちていく様子が見られます。

もうお分かりですね。
地球上では重力があるため、ボールは下方向へ引っ張られる力を受け続けているのです。

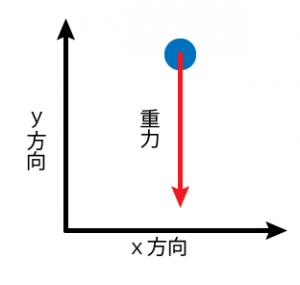
逆に言えば、空気抵抗など、もっと違いはあったりしますが、
そのあたりの細かな点は今回考えないとすれば、
宇宙空間と地球でのボールの運動とでは、重力があるかどうかの違いしかない、ということです。

横方向の動きを考える

ここまで長かったですね！
それではそろそろ、ボールの動きを式に表していきましょう。

まずは簡単な横方向の動きから考えます。

投げられたボールにかかる力を図に表すと、こんな感じですね。

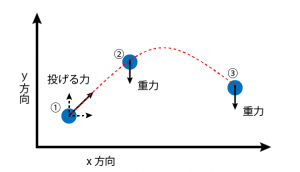
1は投げた瞬間、2，3は投げられた後のボールです。

投げる瞬間はナナメ上に力がかかっていますね。

しかし、2, 3 はどうでしょうか。
重力しかかかっていませんね。

重力は当然ですが、物体を真下に引っ張る力です。
（ただボールを落としたら真横に落ちていった…なんてことは起こりませんよね？）

ということは、ボールに横方向の力がかかるのは、ボールが投げられた瞬間のみ、と言うことになります。
言い換えれば、ボールが飛んでいるときは「横方向に一切の力がかかっていない」と言えるのではないでしょうか。
（もちろん、現実世界では空気抵抗などがあるため横方向の力が存在しますが、とても小さい力のため今回は無視します）

力がかかっていないときの物体の動きは？
先ほど宇宙空間でのボールの動きで考えましたね。
つまり、ボールは「横方向については一定の速度で動いていく」と考えられます。

意外でしたか？
でも、野球ボールを遠投したときのことを考えてみてください。
手を離れたボールが加速したり、いきなり止まったりしないですよね？

ということで、ボールを投げてからの時間を t とすると、
横方向の移動距離 px は

こんな単純な式で表されます。

v0x は x 方向（横方向）の初速度（投げられたときの速度）です。
速度と距離の関係は 距離 = 速度 × 時間 ですので、
横方向の速度と時間をかけ算すれば、横方向のボールの移動距離が出せると言うことになります。

縦方向の動きを考える

さて、横方向の移動距離は最初以外力がかからないため、
とても簡単な式で表すことができました。

次に、縦方向はどうでしょうか。
先ほどの図で確認したように、縦方向には常に重力がかかりつづけることになります。

つまり、力がかかっているため、同じ速度で移動し続けるわけではない、ということですね。

この、「速度がどのように変化するか」について、式で表す必要があります。

そこで必要になるのが「加速度」とよばれるものです。

加速度について簡単にお話しますと、一定の時間でどれだけ速度が変化するかについて表した数値になります。

例えば、アクセルを踏み込んだとき、1 秒あたり 時速 5 km だけ速度が増加する車があるとしましょう。
この車が 時速 20 km から時速 60 km まで加速するのにかかる時間は何秒でしょうか？

…答えは、 60 - 20 = 40 で、時速 40 km の加速が必要なので、1 秒で時速 5 km 加速できるなら
40 / 5 = 8 で 8 秒間かかる、ということになります。

このように、一定の時間（この場合は 1 秒）でどれだけ速度が変化するか（この場合は時速 5 km）というものを表したものが
加速度なのですね。

重力によるボールへの影響も、この加速度を使って考えることができます。

高いところからボールを落とすことを考えてみましょう。
ボールの落下のスピードはドンドン速くなっていく事が予想できますね。
ということは、ボールは重力によって、常に下方向へ加速させられているという事が分かります。

これはボールを上向きに投げたときも同じです。
最初はボールは上向きに飛んでいきますが、ある程度飛んだところで、向きを変えて下に落ちてきますよね。
これは、最初上向きの速度を持っていたボールが、重力によって常に下方向への速度を与えられるため、
徐々に減速し、最終的には下方向へ動くということが起こっているのですね。

加速度と重力の関係について分かったところで、そろそろ式を作っていきましょうか。
ここで重要なのは、速度は徐々に変化していくということです。

先ほどの車の例を考えると分かるのですが、 1 秒あたり 時速 5 km だけ速度が増加する と言っても、
1 秒経過したときに突然時速 20 km で動いていた車が時速 25 km になる…ということはないですよね？

加速度が変化しないとき、速度の変わり方は一定なので、
例の車の速度と時間の関係をグラフに表すと

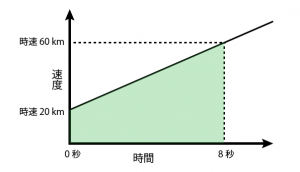
こんな感じ。
0 秒で時速 20 km, 8 秒で時速 60 km で、その間一定で速度が増加していますね。

さて、ここで一つ面白い着眼点を一つ。

一定の速度で動いているものを考えたとき、時間 × 速度は移動距離でしたよね？
これは先ほどの横方向のボールの移動距離を考えたときに使った考えです。

であれば、この図で見たところの、色が塗られた面積が移動距離に該当するということになりますよね？

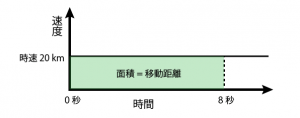
先ほどの図についても面積 = 移動距離として考えて良いのではないでしょうか。

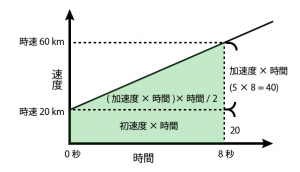
少し複雑ですが、図形を長方形と三角形に分けて考えます。

下の長方形の面積は簡単ですね。
一定の速度で動いているときと同じように、初速度 × 時間 だけでよいです。

上の三角形はどうでしょうか。
三角形の面積は 高さ × 底辺 ÷ 2 で求められますよね。

底辺は時間と同じというのは大丈夫です。
右側の高さはどうでしょうか？

ここで、速度の増加量は、先ほど車の例で計算したように、（加速度 × 時間）でしたね。
ということは、この三角形の高さも、最初の速度からの増加分がそのまま高さになっていますので
（加速度 × 時間）で求められる事になります。

これらをまとめて、図形の面積、すなわち移動距離は
加速度を a とすると

こう表されることになります。

これが、速度が一定で変化する物体の、時間と位置の関係の式になります！

やっとプログラムを書く！

お疲れ様でした！長かったですね！

あとは消化試合みたいなものです。
早速コードを書いてみましょう。

const main = () =＞ {
  const canvas = document.getElementById(’canvas’);
  const ctx = canvas.getContext(’2d’);
  ctx.fillStyle = ’rgb(63, 81, 181)’;


  // -------------- 計算用定数定義 -------------- //
  // 開始時点の時間を取得しておく
  const init_time = new Date();

  // ボールの半径
  const r = 10;

  // ボールの初期座標
  const x = 50;
  const y = 440;

  // ボールの初速度
  const v0x = 30;  // x 方向
  const v0y = -80; // y 方向

  // 重力加速度
  const g = 10;


  // -------------- 描画処理 -------------- //
  const draw = () =＞ {
    ctx.clearRect(0, 0, 640, 480);
    // 現在時刻を取得
    const now = new Date();
    // 開始時点から現在までの経過時間
    const diffSecond = (now.getTime() - init_time.getTime()) * 0.01;

    // 現在の x 軸方向の位置
    const px = x + (v0x * diffSecond);

    // 現在の y 軸方向の位置
    const py = y + ((v0y * diffSecond) + (0.5 * g * diffSecond * diffSecond));

    ctx.beginPath();
    ctx.arc(px, py, r, 0, Math.PI*2, false)
    ctx.fill();

    // 次回画面更新時に draw を実行するように指定
    requestAnimationFrame(draw);
  };

  // 一回目描画実行
  draw();
};

document.addEventListener(’DOMContentLoaded’, main);

前半は計算に使う数字をイイ感じで設定しているだけです。
ちなみに、先ほどまで加速度としてお話していた値については、
重力の場合においてのみ、重力加速度という言い方をします。
記号も加速度では a を使うことが多いですが、重力加速度は g を使います。
（それぞれ英語の頭文字なので、気になる人は調べてみてください）

ちなみに重力加速度は、約秒速 9.8 メートルですが、
数字が細かいですし、今は単位や数値は重要ではないので 10 にしておきます。

また、 const v0y = -80; // y 方向 として、y 方向の初速度がマイナスになっているのは、
canvas では y 方向は下向きであることに由来しています。
今回は投げ上げなので、上方向、つまりマイナス方向に最初の速度を与えてあげる必要があるのですね。

重要なのは

    // 開始時点から現在までの経過時間
    const diffSecond = (now.getTime() - init_time.getTime()) * 0.01;

    // 現在の x 軸方向の位置
    const px = x + (v0x * diffSecond);

    // 現在の y 軸方向の位置
    const py = y + ((v0y * diffSecond) + (0.5 * g * diffSecond * diffSecond));

の部分です。

    // 開始時点から現在までの経過時間
    const diffSecond = (now.getTime() - init_time.getTime()) * 0.01;

ここはいいですね。
単純に、開始時点からの経過時間を取得しています。

    // 現在の x 軸方向の位置
    const px = x + (v0x * diffSecond);

これも大丈夫。
初期位置 + 移動距離 (速度×経過時間) してるだけですね。

    // 現在の y 軸方向の位置
    const py = y + ((v0y * diffSecond) + (0.5 * g * diffSecond * diffSecond));

これももう大丈夫ですね？
なんだか複雑そうに見えますが、式としては px と同じく、初期位置 + 移動距離です。
移動距離は先ほど面積から求める方法で計算できましたよね。
÷ 2 の部分だけ、 0.5 をかけ算する計算に置き換えていますが、そのほかは一緒です。

これを実行すると…

放物線を描くボールのアニメーションができましたね！
お疲れ様でした！

宿題

今回は、ボールを水に投げ込んだときのような様子をアニメーションにしてみましょう。

…とは言っても、先ほどのサンプルとコードはほぼ一緒です。

ポイントとしては

• 重力は下方向にかかっていたが浮力は上方向にかかる
• バックを水色にするには、水色の長方形で塗りつぶしたらよい

この二点が分かれば、後はちょっとした修正だけで行けるはずです！

では、また来週！