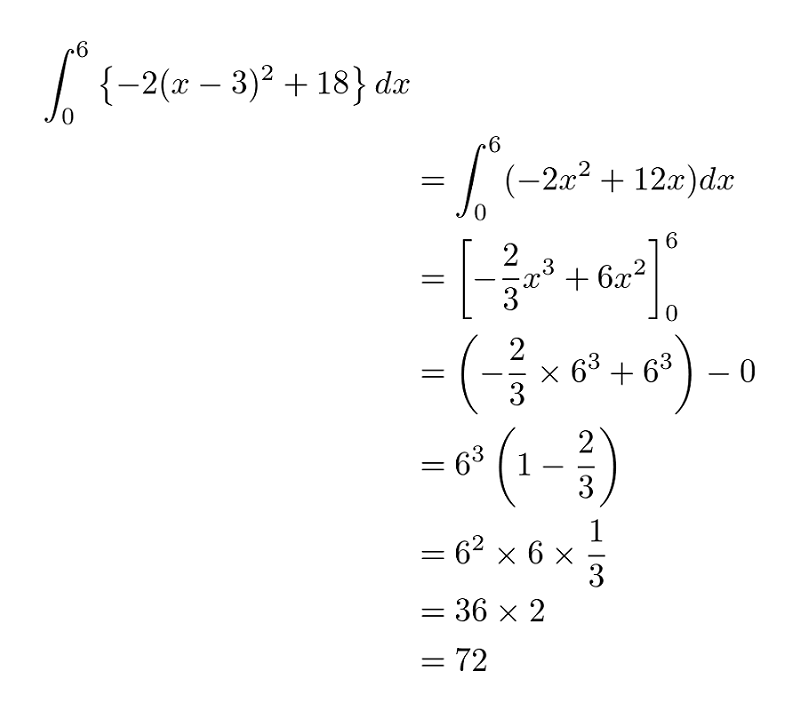どうも、こんにちは。江嵜です。

突然ですが皆さん、積分ってご存知ですか or 覚えてますか？
現在では高校の数IIで学び始める内容ですね。

軽くご説明しますと、ある数式で作れるグラフに囲まれた領域の面積を求める方法が積分です。
（定積分と呼ばれるヤツですね）

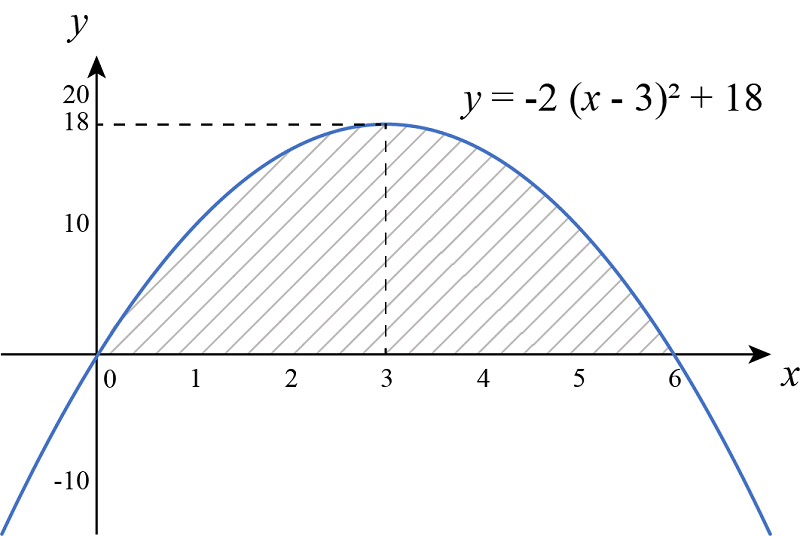
例えば、「下のグラフの斜線部分の面積を求めてみましょう」という問題であれば、
定積分で一撃、なのですが…。

本当にその答えって面積になっているのかな…？という疑問を持ったことがある方もいらっしゃるのでは。
今回はそんな疑問を解決するべく、プログラミングの力を使い、別のアプローチで面積を求めてみましょう。

まずは普通に定積分の計算をしてみる

今回は「本当に積分の答えは面積を表しているのか」を調べるので、先に積分で出る答えを確認しておきましょう。

72 と出ましたね！
と、これは高校の授業でよくある計算です。

モンテカルロ法で面積を求めるぞ！

それでは、ここからが本題。
先程求めた面積を、プログラミングの力で別のアプローチから求めてみましょう。

今回は モンテカルロ法 と呼ばれる手法を利用して、面積を求めてみましょう。

モンテカルロ法とは？

モンテカルロ法を初めて聞く方も多いと思うので、少し解説いたしますね。
モンテカルロといえば、カジノで有名なあのモンテカルロですね！
この方法は、まさにルーレットのように、ランダムな数字の性質を使って行う計算です。

例えば、普通のサイコロを思い浮かべてそれを何度も投げることを考えます。
サイコロは 1 ~ 6 までの数字がランダムに出て、次の目が何になるかは誰にも分からないですよね。
しかし、これを何百・何千・何万回と繰り返していくと、それぞれの目が出る割合は
ちょうど 1/6 ずつになっていくことが知られています。
（ 1 だけ沢山出る、みたいなことはないということですね）

モンテカルロ法はこのように、ランダムな数字をたくさん発生させた時、その偏りが少なくなっていく性質を利用したものです。

今回の考え方

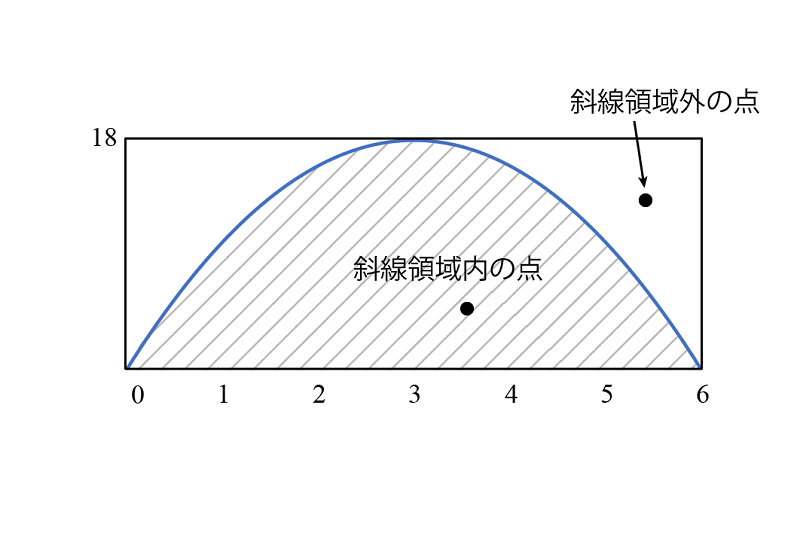
今回は、面積を求めたい領域(斜線部分)がすっぽり入る四角形を考えて（黒い枠部分）、その中に適当に点を一つ打ちます。
そして、その点が斜線部分に入っているか、入っていないかを確認します。

これを何度も繰り返していくと、四角形の中に均等に点が打たれていくので、
四角形の面積 : 求めたい面積 = 点が四角形の中に打たれる確率(100%) ： 点が斜線部分に打たれる確率
すなわち、
四角形の面積 : 求めたい面積 = 打った点の数 ： 斜線部分に入った点の数
の比の式が成り立つだろう、という事を利用して面積を求めていきます。

ひたすら点を取り、その位置を確認することを繰り返す、ゴリ押し解法ですね。

JavaScript で計算してみた

実際に JavaScript でコードを書いてみるとこんな感じ。

// y の値を求める式
const fx = (x) => {
    return ((-1)*2*x*x) + (12*x);
};

// 四角形の横幅
const width = 6.0;
// 四角形の高さ
const height = 18.0;
// 点を打つ回数
const times = 100000;

// 点が斜線領域内に入った回数
let in_dot = 0;

for (let i = 0; i < times; i++) {
    // ランダムな点の横方向位置
    const dot_x = Math.random() * width;
    // ランダムな点の縦方向位置
    const dot_y = Math.random() * height;
    // グラフの縦方向の位置
    const graph_y = fx(dot_x);

    // 点がグラフの線より低い位置にあれば（斜線内にあれば）
    if (dot_y < graph_y) {
        // 斜線内領域に入った回数を 1 増やす
        in_dot++;
    }
}

// 比の計算
const result = width * height * in_dot / times;
console.log(result);

点が斜線領域内かどうかを判別するところが少しだけ難しいかもしれないですね。
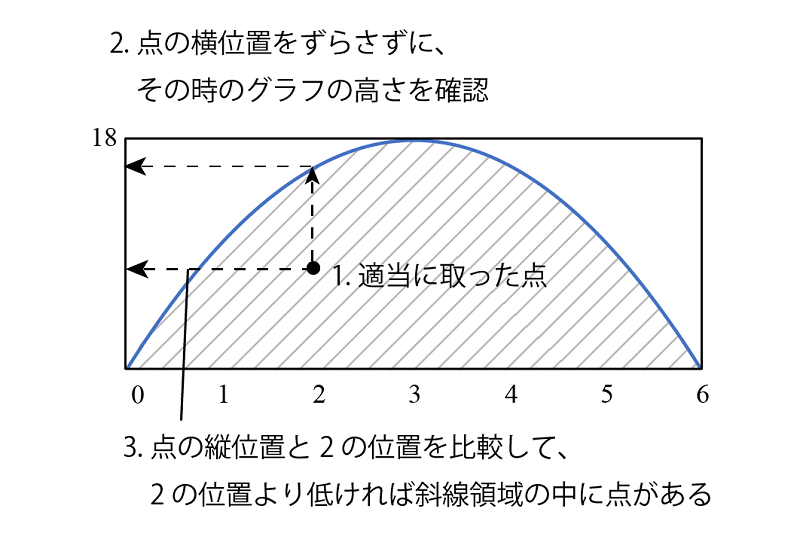
考え方としては、
1. 適当に点を取る
1. 点の横方向(x方向)の値を取り、その時の領域の一番上の高さを求める
1. 適当に取った点が 2 の高さより低ければ、斜線の領域に入っている
となります。

試しに5回実行してみると、結果は…

71.86644
72.01764
71.91504
72.24444
71.82648

ほぼ 72 付近ですね！
（ランダムな数が完全に均等にはならないので、どうしてもばらつきが出てしまいますが）
やはり積分の計算というのは、面積を求めることが出来るみたいです。

ちなみに、点を打つ回数を増やしていくことで、精度は上がっていきます。
上の結果はそれぞれ 10 万回の点を売った場合の結果ですが、その 100 倍にあたる、 1 億回の点を取ってみると…

71.99322228
71.9937342
72.0020826
71.99869572
71.99368452

と、かなり精度が上がっていることが分かりますね！
やっぱり面積は 72 で合っていそうです！

終わりに

プログラミングの力で積分をゴリ押しする技、いかがでしたでしょうか。
数学の解放は一つじゃない！とよく言いますが、こんな解き方もちょっと面白いですよね。
（もちろん、テスト時間に PC を持ち込む訳にはいきませんが）

皆さんも手元でプログラムを動かしてみてくださいね。